Ученый Политеха сформулировал новую математическую модель

Она позволит описать высокоинтенсивные колебания систем с подвижными границами

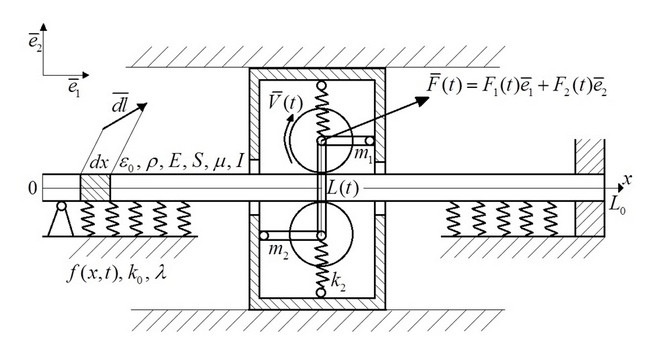
Среди всех многочисленных задач по динамике упругих систем особо выделяются задачи о колебаниях в системах с подвижными границами: продольно-поперечные колебания канатов грузоподъемных установок, гибких звеньев передач, стержней твердого топлива и балок переменной длины, бурильных колонн, железнодорожной контактной сети, ленточных конвейеров и т.д. До сих пор не существует общего подхода к постановке таких задач. Заведующий кафедрой «Общетеоретические дисциплины» сызранского филиала Политеха Владислав Литвинов разработал новую нелинейную математическую модель, с помощью которой можно будет описывать высокоинтенсивные колебания систем с подвижными границами.

– Как правило, говоря о колебаниях в системах с подвижными границами, ученые в каждом конкретном случае адаптируют существующие методы для решения рассматриваемой задачи уравнений в изменяющихся геометрических областях. Но они качественно отличаются от классических методов математической физики, а значит, при расчетах возможна погрешность, которая может привести к серьезным последствиям, например, несчастным случаям, – поясняет Литвинов.

Ученый Политеха уже много лет работает над анализом резонансных свойств, возникающих при колебаниях большой интенсивности – будь то трос подъемника кабины лифта, буровой инструмент, ременная передача, рельсовые пути и т.д. Цель его исследований – повышение надежности работы технических объектов с переменными во времени границами, повышение точности расчетов конструкций на динамическую прочность.

Совсем недавно он описал новую нелинейную математическую модель поперечных колебаний вязкоупругой балки с подвижной подпружиненной опорой, несущей присоединенную массу. С ее помощью можно рассчитать граничные условия, в которых взаимодействуют части объекта слева и справа от подвижной границы с учетом обмена энергией через нее и, следовательно, избежать непредвиденных ситуаций.

Кстати, Владислав Литвинов вошел в перечень 40 авторов, имеющих наибольшее количество публикаций на Общероссийском математическом портале Math-Net.Ru.